Spice - модели электронной компонентной базы
При схемотехническом моделировании электронная компонентная база (ЭКБ), из которой составляется электрическая принципиальная схема, заменяется математическими моделями двух типов:
1. Встроенные в программы схемотехнического моделирования математические модели стандартных компонентов, таких как резисторы, конденсаторы, диоды, биполярные и полевые транзисторы, независимые источники сигналов и др., которые не могут быть изменены пользователями; можно только изменять значения их параметров.
2. Модели в виде подсхем, представленных в формате SPICE, поскольку подавляющее большинство библиотек ЭКБ используют именно этот формат, он же является стандартом для описания моделей, предоставляемых производителями ЭКБ.
Здесь мы рассмотрим, в первую очередь встроенные в программы Spice – модели ЭКБ.
Резистор
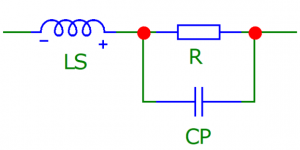
На высоких частотах резисторы перестают быть резисторами в чистом виде, а паразитные элементы в реальных компонентах влияют на их значения. Когда частоты достигают сотен мегагерц, базовые компоненты, такие как резисторы, катушки индуктивности и конденсаторы, приобретают неидеальные характеристики. Такие изменения могут стать критическими при проектировании фильтров, схем питания и т.д
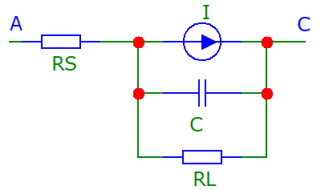
На рисунке представлена полная модель резистора, учитывающая паразитную индуктивность выводов и параллельную емкость между торцевыми крышками. Эта модель справедлива на высоких частотах.
Таблица. Параметры модели резистора
| Название | Параметр | Единицы измерения |
| LS | Паразитная индуктивность | Гн |
| CP | Паразитная емкость | Ф |
| TC1 | Линейный температурный коэффициент | 1/ºC |
| TC2 | Квадратичный температурный коэффициент | 1/ºC |
| T_MEASURED | Температура измерения | ºC |
На рисунке 1 показана зависимость импеданса от частоты для резистора номиналом 1 мОм с паразитными индуктивностью LS=1нГн и емкостью CP=0.2пФ.
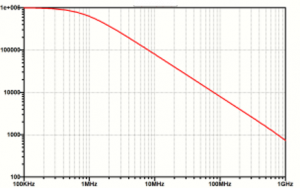
Рис. 1
Конденсатор
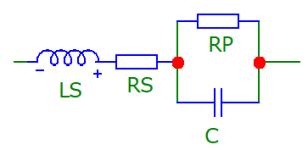
С увеличением частоты характеристики катушек индуктивности и конденсаторов изменяются. На высоких частотах конденсаторы могут начать вести себя как катушки индуктивности и наоборот.
На рисунке представлена модель SPICE, которая моделирует частотно-зависимое поведение конденсаторов. Модель основана на графике зависимости импеданса от частоты конденсаторов, которые приводятся в техническом описании конденсаторов.
Таблица. Параметры модели конденсатор
| Название | Параметр | Единицы измерения |
| LS | Паразитная индуктивность | Гн |
| RP | Паразитное сопротивление | Ф |
| RS | Паразитное сопротивление выводов | Гн |
| TC1 | Линейный температурный коэффициент | 1/ºC |
| TC2 | Квадратичный температурный коэффициент | 1/ºC |
| T_MEASURED | Температура измерения | ºC |
Работу модели проиллюстрируем на примере конденсатора типа GRM1552C1H121GA01 от компании muRata.
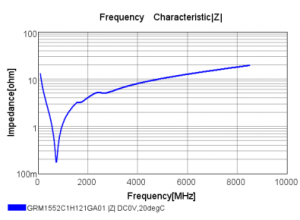Рис. 1
На рисунке 1 представлена зависимость импеданса от частоты из технического описания конденсатора. Она носит резонансный характер, определяемый паразитными параметрами LS, RS и емкостью конденсатора С. Величина импеданса на резонансной частоте равна паразитному сопротивлению RS и составляет 0.2 Ом. Последовательная паразитная индуктивность LS получена из формулы последовательного резонанса и равна 375 pH.
На рисунке 2 представлены результаты моделирования зависимости импеданса от частоты.
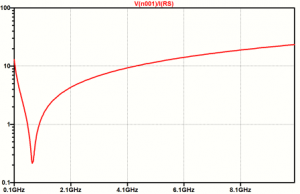Рис. 20ю
Катушка индуктивности
Моделирование индуктивных элементов в SPICE всегда не имело большого значения для разработчиков аналоговых устройств. Отчасти это объясняется тем, что SPICE был разработан в первую очередь для моделирования интегральных схем, в которых индуктивные элементы обычно являются паразитными и очень маленькими, что позволяло использовать идеальные модели индуктивностей.
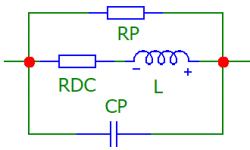
Применение SPICE для проектирования дискретных аналоговых схем таких как импульсные источники питания и фильтры, в поведении которых индуктивные элементы имеют решающее значение для точности моделирования, привело к необходимости использования более точных моделей индуктивностей. Такая модель представлена на рисунке.
| Название | Параметр | Единицы измерения |
| RDC | Сопротивление на постоянном токе | Ом |
| RP | Сопротивление, учитывающее потери в сердечнике | Ом |
| CP | Паразитная емкость | Ф |
| TC1 | Линейный температурный коэффициент | 1/ºC |
| TC1 | Квадратичный температурный коэффициент | 1/ºC |
| T_MEASURED | Температура измерения | ºC |
Работу модели проиллюстрируем на примере катушки индуктивности DFE21CCN1R0MEL от компании muRata
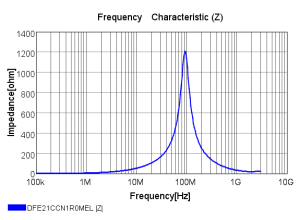Рис. 1.
На рисунке 1 представлена зависимость импеданса от частоты из технического описания катушки индуктивности. Она носит резонансный характер, определяемый параметрами CP, RDC и индуктивностью L. Величина импеданса на резонансной частоте равна сопротивлению RP и составляет 1.2 кОм. Паразитная емкость Cp определяются из резонансной частоты и равна 2.99 пФ. Сопротивление RDC приводится в паспортных данных на индуктивность.
На рисунке 2 представлены результаты моделирования зависимости импеданса от частоты.
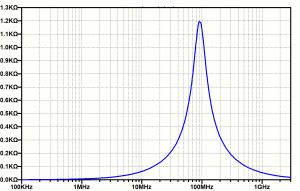Рис. 2
Диод
Модель диода основана на характеристиках , описанных в техническом паспорте изделия и характеристиках производственного процесса. Ниже в таблице приведены параметры SPICE-модели диода. Получить параметры модели можно несколькими способами. Первый способ заключается в проведении измерений реального устройства и последующего расчета параметров модели, второй – определение параметров на основе характеристик, приведенных в техническом паспорте на прибор, а третий, самый простой, обратиться к веб-сайту производителя и скачать модель.
Таблица. Параметры модели диода
| Название | Параметр | Единицы измерения |
| IS | Ток насыщения | A |
| RS | Объемное сопротивление | Ω |
| N | Коэффициент неидеальности | – |
| TT | Время переноса заряда | c |
| CJO | Барьерная емкость при нулевом смещении | Ф |
| VJ | Контактная разность потенциалов | В |
| M | Коэффициент плавности перехода | – |
| EG | Ширина запрещенной зоны | эВ |
| XTI | Температурный коэффициент тока насыщения | – |
| KF | Коэффициент фликкер – шума | – |
| AF | Показатель степени фликкер – шума | – |
| FC | Коэффициент нелинейности барьерной емкости прямосмещенного перехода | – |
| BV | Напряжение обратного пробоя | В |
| IBV | Начальный ток пробоя | A |
| TNOM | Номинальная температура | °C |
Работу модели рассмотрим на примере диода 1N4001 от компании Vishay и воспользуемся моделью, приведенной на их сайте. На рисунке 1 представлены вольт-амперная и вольт-фарадная характеристики диода 1N4001, представленные в техническом паспорте.
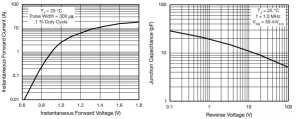Рис. 1
Для моделирования этих характеристик воспользуемся моделью, приведенной на сайте производителя.
.MODEL D1n4001rl d(IS=5.31656e-08 RS=0.0392384 N=2 EG=0.6 XTI=0.05 BV=400 IBV=5e-08 CJO=31p VJ=0.7 M=0.5 +FC=0.5 TT=1e-09 KF=0 AF=1)
На рисунке 2 представлены расчетные вольт-амперная и вольт-фарадная характеристики.
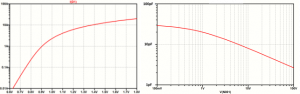Рис. 2
Биполярный транзистор
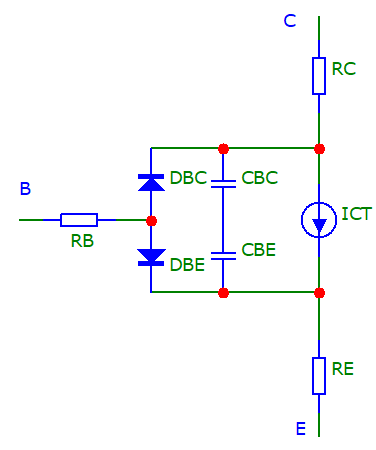
Для схемотехнического моделирования в качестве Spice-модели биполярного транзистора обычно применяют модель Гуммеля–Пуна (Gummel H.K., Poon H.C.) Упрощённая модель Гуммеля–Пуна приведена на рисунке, а ее параметры в таблице. Аналогично модели диода существуют три способа получения параметров модели: первый, на основе экспериментальных измерений характеристик транзистора, второй, на основе информации из технического паспорта, а третий, воспользоваться моделью от производителя.
Таблица. Параметры модели биполярного транзистора
| Название | Параметр | Единицы измерения |
| IS | Ток насыщения. | A |
| BF | Максимальный коэффициент усиления тока базы в нормальном режиме в схеме с ОЭ. | – |
| NF | Коэффициент неидеальности перехода в нормальном режиме. | – |
| VAF | Напряжение Эрли в номальном режиме. | В |
| IKF | Ток начала спада зависимости BF от тока коллектора в нормальном режиме. | A |
| ISE | Обратный ток эмиттерного перехода. | A |
| NE | Коэффициент неидеальности эмиттерного перехода в нормальном режиме. | – |
| BR | Максимальный коэффициент усиления тока базы в инверсном режиме в схеме с ОЭ. | – |
| NR | Коэффициент неидеальности перехода в инверсном режиме. | – |
| VAR | Напряжение Эрли в инверсном режиме. | В |
| IKR | Ток начала спада зависимости BF от тока эмиттера в инверсном режиме. | A |
| ISC | Обратный ток коллекторного перехода. | A |
| NC | Коэффициент неидеальности коллекторного перехода в нормальном режиме. | – |
| RB | Объемное сопротивление базы. | Ω |
| IRB | Ток базы, при котором сопротивление базы Rb уменьшается на 50% полного перепада между RB и RBM. | A |
| RBM | Минимальное сопротивление базы при больших токах. | Ω |
| RE | Объемное сопротивление эмиттера. | Ω |
| RC | Объемное сопротивление коллектора. | Ω |
| CJE | Емкость эмиттерного перехода при нулевом смещении. | Ф |
| VJE | Контактная разность потенциалов перехода база-эмиттер. | В |
| MJE | Коэффициент, учитывающий плавность эмиттерного перехода. | – |
| TF | Время переноса заряда через базу в нормальном режиме. | С |
| XTF | Коэффициент, определяющий зависимость TF от смещения база-коллектор. | – |
| VTF | Напряжение, характеризующее зависимость TF от смещения база-коллектор. | В |
| ITF | Ток, характеризующий зависимость TF от тока коллектора при больших токах. | A |
| PTF | Дополнительный фазовый сдвиг на граничной частоте транзистора freq=1.0/(TF*2PI) Гц. | град. |
| CJC | Емкость коллекторного перехода при нулевом смещении. | Ф |
| VJC | Контактная разность потенциалов перехода база-коллектор. | В |
| MJC | Коэффициент, учитывающий плавность коллекторного перехода. | – |
| XCJC | Коэффициент расщепления емкости база – коллектор. | – |
| TR | Время переноса заряда через базу в инверсном режиме. | C |
| CJS | Емкость коллектор-подложка при нулевом смещении. | Ф |
| VJS | Контактная разность потенциалов перехода коллектор-подложка. | В |
| MJS | Коэффициент, учитывающий плавность перехода коллектор-подложка. | – |
| XTB | Температурный коэффициент BF и BR. | – |
| EG | Ширина запрещенной зоны. | эВ |
| XTI | Температурный коэффициент IS. | – |
| KF | Коэффициент, определяющий спектральную плотность фликкер-шума. | – |
| AF | Показатель степени фликкер – шума. | – |
| FC | Коэффициент нелинейности барьерных емкостей прямосмещенных переходов. | – |
| TNOM | Номинальная температура | °C |
Работу модели проиллюстрируем на примере транзистора КТ503А. Для моделирования его характеристик воспользуемся следующей моделью.
.MODEL KT503A NPN(Is=6.843f Xti=3 Eg=1.11 Vaf=60 Bf=124.8 Ise=70.91f Ne=1.372 Ikf=.4526 Nk=.5243 Xtb=1.5 Br=1.1 Isc=26.4p Nc=2.088 Ikr=1.637 Rb=12 Rc=1.538 Cjc=23.66p Mjc=.33 Vjc=.75 Fc=.5 Cje=30.84p Mje=.33 Vje=.75 Tr=648.9n Tf=10.09n Itf=1 Xtf=2 Vtf=10)
На рисунке 1 представлены зависимость статического коэффициента усиления от тока базы, представленная в техническом паспорте на компонент и расчетная зависимость по его модели.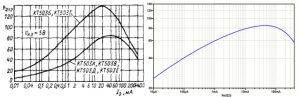
Полевой транзистор
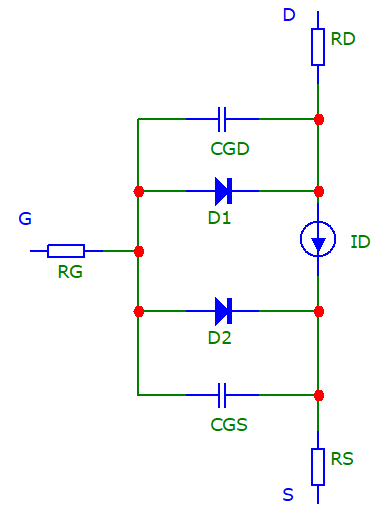
Полевой транзистор – полупроводниковый прибор, работа которого основана на управлении электрическим сопротивлением токопроводящего канала поперечным электрическим полем, создаваемым приложенным к затвору напряжением. Так же, как и биполярные транзисторы полевые транзисторы применяются в электронных устройствах для усиления или генерации электрических колебаний. На рисунке представлена модель полевого транзистора, а ее параметры в таблице.
Таблица. Параметры модели полевого транзистора
| Название | Параметр | Единицы измерения |
| VTO | Пороговое напряжение. | В |
| BETA | Коэффициент пропорциональности. | A/В2 |
| LAMBDA | Параметр модуляции длины канала. | 1/В |
| RD | Объемное сопротивление области стока. | Ω |
| RS | Объемное сопротивление области истока. | Ω |
| CGS | Емкость перехода затвор-исток при нулевом смещении. | Ф |
| CGD | Емкость перехода затвор-сток при нулевом смещении. | Ф |
| PB | Контактная разность потенциалов p-n перехода затвора | В |
| IS | Ток насыщения p-n перехода затвор-канал | A |
| KF | Коэффициент, определяющий спектральную плотность фликкер-шума. | – |
| AF | Показатель степени фликкер – шума. | – |
| FC | Коэффициент нелинейности емкостей переходов при прямом смещении. | – |
| TNOM | Номинальная температура | °C |
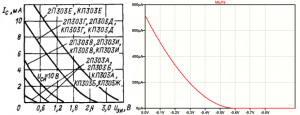
Работу модели проиллюстрируем на примере транзистора КП303А. Для моделирования его характеристик воспользуемся следующей моделью.
.MODEL KP303A njf (vt0=-0.6 beta=1.6m lambda=0.02 rd=30 rs=35 cgs=5p cgd=4p is=100f B=1.2 kf=1.e-16 af=1.4 MFG=USSR)
На рисунке 1 представлены зависимость тока стока от напряжения затвор – исток, представленная в техническом паспорте на компонент и расчетная зависимость по его модели.
Операционный усилитель
Уровень 1
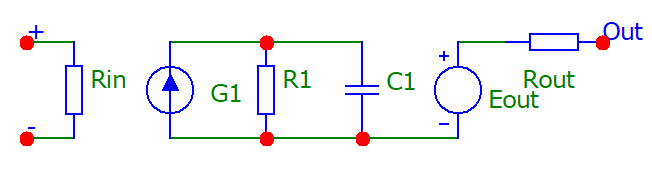
SPICE-модели операционных усилителей различаются по сложности от нескольких до 100 и более компонентов. Все зависит от того, что необходимо моделировать только основные характеристики или тонкие особенности поведения операционного усилителя. Базовая модель первого уровня включает всего несколько компонентов и отображает основные характеристики ОУ.
Таблица. Параметры модели операционного усилителя
| Название | Параметр | Единицы измерения |
| Rin | Входное сопротивление | Ом |
| Rout | Выходное сопротивление | Ом |
| F0 | Частота единичного усиления | Гц |
| Ku | Коэффициент усиления без обратной связи | – |
Работу модели рассмотрим на примере операционного усилителя 140УД1А. На основе данных технического паспорта синтезируем его SPICE-модель.
***********************************************
* SPICE МОДЕЛЬ ОУ - Уровень 1
* Subckt Name: 140УД1А
***********************************************
* Контакты Вх+ Вх- Вых.
.SUBCKT 140УД1А 1 2 82
* Входное сопротивление
Rin 1 2 5.00000e+04
* Каскад усиления: Коэффициент усиления, Частота первого полюса АЧХ
* Ku=4.50000e+03, Fp1=2.22222e+01 Гц
G1 0 10 VALUE = { 4.50000e-03 * V(1,2) }
R1 10 0 1.00000e+06
C1 10 0 7.16197e-09
* Выходной каскад
EOUT 80 0 10 0 1
ROUT 80 82 3.00000e+02
.ENDSРассчитанные с использование полученной модели графики АЧХ и скорости нарастания выходного напряжения представлены на рисунке 1.
Рис. 1
Уровень 2
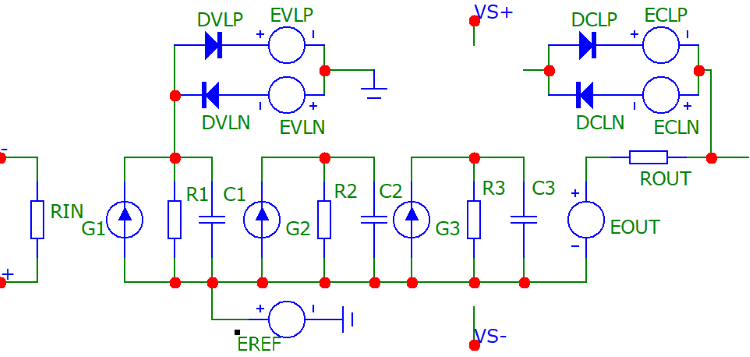
Модель второго уровня учитывает частотные свойства операционного усилителя, ограничение скорости нарастания и предельные значения выходного напряжения/тока.
| Название | Параметр | Единицы измерения |
| Rin | Входное сопротивление | Ом |
| Rout | Выходное сопротивление | Ом |
| F0 | Частота единичного усиления | Гц |
| Ku | Коэффициент усиления без обратной связи | – |
| Slew | Скорость нарастания выходного напряжения | В/мкс |
| V0 Lim | Ограничение выходного напряжения | В |
| I0 Lim | Максимальный выходной ток | А |